 11.3 CSG
11.3 CSG

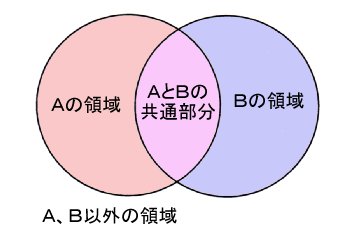
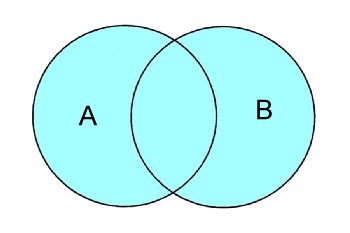
 11.3-1 論理和(union)
11.3-1 論理和(union)
union{
OBJECT_A
OBJECT_B
...
[ texture { ... } ]
[ MODFIERS ... ]
}
|
||
| union | 論理和を指定するためのキーワード。 | |
| OBJECT_A OBJECT_B ... |
要素となる物体の指定。 物体ごとにテクスチャや変形などを指定で きる。 |
|
| texture { ... } | 全体のテクスチャの指定。 | |
| MODFIERS ... | 変形などの指定。 | |
●論理和の例(図11.3-1b)
union {
cone{x*-1.8,1.5,x*1.5,0.5
texture{Bump_Check}
}
sphere{x,1.8
texture{Bump_Leopard}
}
clipped_by{plane{z,0}}
}
|
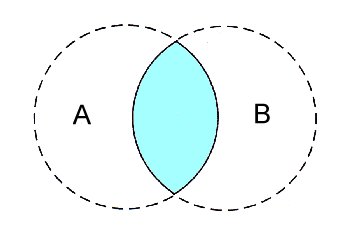
 11.3-2 論理積(intersaction)
11.3-2 論理積(intersaction)
intersection{
OBJECT_A
OBJECT_B
...
[ texture { ... } ]
[ MODFIERS ... ]
}
|
||
| intersection | 論理積を指定するためのキーワード。 | |
| OBJECT_A OBJECT_B ... |
要素となる物体の指定。 物体ごとにテクスチャや変形などを指定で きる。 |
|
| texture { ... } | 全体のテクスチャの指定。 | |
| MODFIERS ... | 変形などの指定。 | |
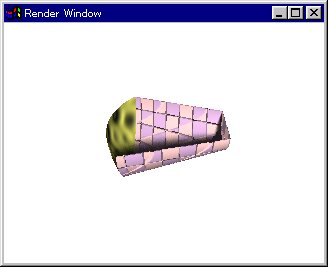
●論理積の例(図11.3-2b)
intersection {
cone{x*-1.8,1.5,x*1.5,0.5
texture{Bump_Check}
}
sphere{x,1.8
texture{Bump_Leopard}
}
clipped_by{plane{z,0}}
}
|
 11.3-3 論理差(difference)
11.3-3 論理差(difference)
difference{
OBJECT_A
OBJECT_B
...
[ texture { ... } ]
[ MODFIERS ... ]
} |
||
| difference | 論理差を指定するためのキーワード。 | |
| OBJECT_A OBJECT_B ... |
要素となる物体の指定。 物体ごとにテクスチャや変形などを指定で きる。 最初に指定した物体から、その後に指定した物体との共通 部分が切り取られる。 |
|
| texture { ... } | 全体のテクスチャの指定。 | |
| MODFIERS ... | 変形などの指定。 | |
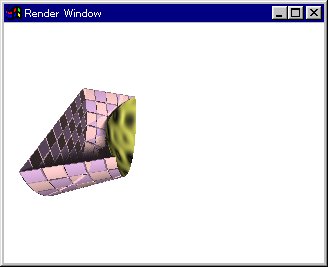
●論理差の例(図11.3-3b)
difference {
cone{x*-1.8,1.5,x*1.5,0.5
texture{Bump_Check}
}
sphere{x,1.8
texture{Bump_Leopard}
}
clipped_by{plane{z,0}}
}
|
 11.3-4 マージ(merge)
11.3-4 マージ(merge)
merge {
OBJECT_A
OBJECT_B
...
[ texture { ... } ]
[ MODFIERS ... ]
}
|
||
| difference | マージを指定するためのキーワード。 | |
| OBJECT_A OBJECT_B ... |
要素となる物体の指定。 物体ごとにテクスチャや変形などを指定で きる。 |
|
| texture { ... } | 全体のテクスチャの指定。 | |
| MODFIERS ... | 変形などの指定。 | |
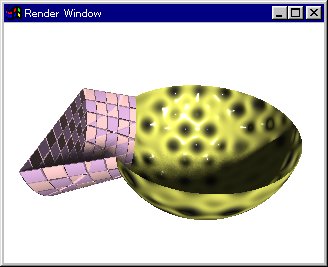
●マージの例(図11.3-4b)
merge {
cone{x*-1.8,1.5,x*1.5,0.5
texture{Bump_Check}
}
sphere{x,1.8
texture{Bump_Leopard}
}
clipped_by{plane{z,0}}
}
|

 11.4 物体のオプション
11.4 物体のオプション
 11.4-1 クリッピング(clipped_by)
11.4-1 クリッピング(clipped_by)

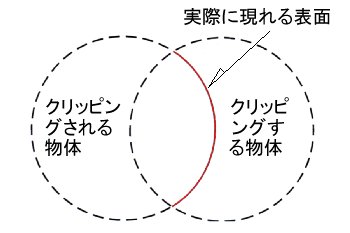
object {
OBJECT
clipped_by{ CLIPPING_OBJECT } | clipped_by { bounded_by }
}
|
||
| object | 物体を指定するためのキーワード。 物体識別子を使うとき以 外は省略してもよい。 |
|
| OBJECT | クリッピングされる物体の指定。 どんな物体でも指定できる。 | |
| clipped_by | クリッピングを指定するキーワード | |
| CLIPPING_OBJECT | クリッピング形状の指定。 ※ 有限パッチ形状は使用できない。⇒「8.1 プリミティブ」 |
|
| bounded_by | バウンディング物体をクリッピングに使用する指定 | |
object {
cylinder { <-5,0.5,0.5>, <5,0.5,0.5>, 0.3 pigment{color rgb 0.8} }
bounded_by { box { <0,0,0>, <1,1,1> pigment{color rgb 0.5} } }
clipped_by { bounded_by }
}
 11.4-2 バウンディング(bounded_by)
11.4-2 バウンディング(bounded_by)
object {
OBJECT
bounded_by{ BOUNDING_OBJECT } | bounded_by { clipped_by }
}
|
||
| object | 物体を指定するためのキーワード。 物体識別子を使うとき以 外は省略してもよい。 |
|
| OBJECT | バウンディングされる物体の指定。 | |
| bounded_by | バウンディングを指定するキーワード。 | |
| BOUNDING_OBJECT | バウンディング形状の指定。 球やボックスなど、単純な形状 を指定する。 ※ 有限パッチ形状は使用できない。⇒「11.1 プリミティブ」 |
|
| bounded_by | クリッピング物体をバウンディングに使用する指定 | |
object {
cylinder { <-5,0.5,0.5>, <5,0.5,0.5>, 0.3 pigment{color rgb 0.8} }
clipped_by { box { <0,0,0>, <1,1,1> pigment{color rgb 0.5} } }
bounded_by{ clipped_by }
}
 11.4-3 中空(hollow)
11.4-3 中空(hollow)
object {
OBJECT
hollow
}
|
||
| object | 物体を指定するためのキーワード。 物体識別子を使うとき以 外は省略してもよい。 |
|
| OBJECT | 内部に大気効果を含む物体。 | |
| hollow | 物体内部を中空にするためのキーワード。 | |
union {
sphere { -0.5*x, 1 }
sphere { 0.5*x, 1 }>
hollow
}
union {
sphere { -0.5*x, 1 hollow off }
sphere { 0.5*x, 1 }
hollow
}
 11.4-4 物体の影スイッチ(no_shadow)
11.4-4 物体の影スイッチ(no_shadow)
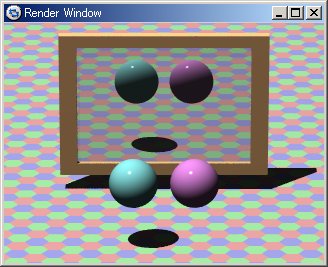
● no_shadowの例(図11.4-4)
sphere{
<-0.5,0,0.1>,0.4
no_shadow
texture{finish{Shiny} pigment{color rgb<1,0.6,1>} }
}
sphere{
<0.5,0,0.1>,0.4
texture{finish{Shiny} pigment{color rgb<0.6,1,1>} }
}
|
 11.4-5 物体のイメージスイッチ(no_image)
11.4-5 物体のイメージスイッチ(no_image)
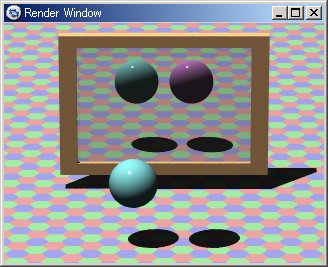
● no_imageの例(図11.4-5)
sphere{
<-0.5,0,0.1>,0.4
no_image
texture{finish{Shiny} pigment{color rgb<1,0.6,1>} }
}
sphere{
<0.5,0,0.1>,0.4
texture{finish{Shiny} pigment{color rgb<0.6,1,1>} }
}
|
 11.4-6 物体の鏡面反射スイッチ(no_reflection)
11.4-6 物体の鏡面反射スイッチ(no_reflection)
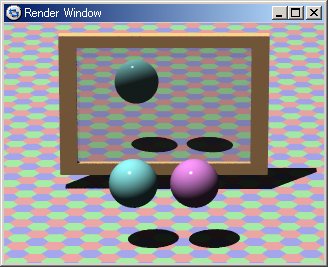
● no_reflectionの例(図11.4-6)
sphere{
<-0.5,0,0.1>,0.4
no_reflection
texture{finish{Shiny} pigment{color rgb<1,0.6,1>} }
}
sphere{
<0.5,0,0.1>,0.4
texture{finish{Shiny} pigment{color rgb<0.6,1,1>} }
}
|
 11.4-7 両面照明(double_illuminate)
11.4-7 両面照明(double_illuminate)
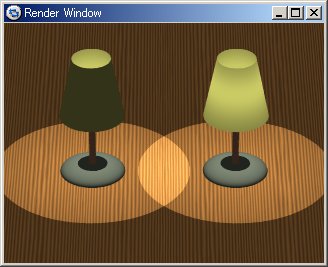
● double_illuminateの例(図11.4-7)
#declare LUMP=union{
cone{<0,0,1>,0.5,<0,0,2>,0.3 open
pigment{ color <1,1,0.5>} }
light_source{<0,0,1.5> color 1}
}
#declare LEG=union{
cylinder{<0,0,0>,<0,0,1.2>,0.05 pigment{ color <1,0.7,0.5>} }
sphere{<0,0,0>,0.5 scale 0.3*z pigment{ color <0.65,0.7,0.6>} }
}
#declare LSTAND1=union{object{LUMP} object{LEG} }
#declare LSTAND2=union{object{LUMP double_illuminate} object{LEG} }
object{LSTAND1 translate x*1.1}
object{LSTAND2 double_illuminate translate x*-1.1}
|
 11.4-8 マテリアル(material)
11.4-8 マテリアル(material)
● materialの例
#declare MyGlass = material{ texture{ Glass_T } interior{ Glass_I } }
sphere{z*3, 1 material{ MyGlass } }
|
 11.4-9 インバース(inverse)
11.4-9 インバース(inverse)
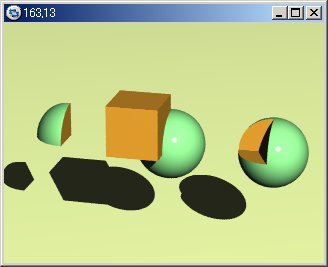
左側:球とボックスの論理積 中央:球とボックスの論理和 右側:球とボックス(inberse)の論理積 |
● インバースの例(図11.4-9)
//-------------------Left
intersection{
sphere{<0,0,0>,1
texture{ finish{Shiny} pigment{color rgb<0.6,1,0.6>} } }
box{<0,0,0><1.5,1.5,1.5> pigment{color rgb<1,0.7,0.2>} }
translate x*3
}
//------------------Center
union{
sphere{<0,0,0>,1
texture{ finish{Shiny} pigment{color rgb<0.6,1,0.6>} } }
box{<0,0,0><1.5,1.5,1.5> pigment{color rgb<1,0.7,0.2>} }
}
//------------------Right
intersection{
sphere{<0,0,0>,1
texture{ finish{Shiny} pigment{color rgb<0.6,1,0.6>} } }
box{<0,0,0><1.5,1.5,1.5> inverse pigment{color rgb<1,0.7,0.2>} }
translate x*-3
}
|
 11.4-10 曲面の高精度計算(sturm)
11.4-10 曲面の高精度計算(sturm)
object {
OBJECT
sturm
}
|
||
| object | 物体を指定するためのキーワード。 物体識別子を使うとき以 外は省略してもよい。 |
|
| OBJECT | 高次多項式による形状。 次のものが使用できる。 ●簡易回転体(sor) ●回転体(lathe;2次スプラインのみ) ●角柱(prism;3次スプラインのみ) ●ブロブ(blob) ●3次曲面(cubic) ●4次曲面(quartic) ●高次曲面(poly) | |
| sturm | 曲面の計算を高精度にするためのキーワード。 | |