三次元音場の固有モード

5.1　直方体室の固有振動

一般の室内では、三次元の空間の中の音波を考えねばならない。Chapter 1 で述べたように、平面波に関する三次元の波動方程式は、

Ｃ：音速

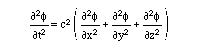
である。三次元の速度ポテンシャルは、この解として与えられる。（ 三次元の速度ポテンシャル）

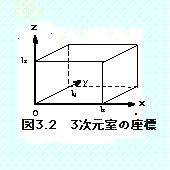いま、図のように各辺の長さがｌx、ｌy、ｌzの直方体の室を考える。その周壁が全て剛壁の場合、境界条件は壁面上で壁に垂直方向の粒子速度が０、である。この条件下で三次元の固有周波数を求めると、

一次元の固有周波数

と同様、
ただし、ｎx, ｎy, ｎz　はそれぞれ０、１、２、３．．．となる。一次元の粒子速度の室内分布
と同様に、その粒子速度の室内分布は定在波として
で表わされ、音圧分布も、一次元の分布
と同様に、
の定在波で表わされる。また音圧の式は、
となる。なお、音圧は粒子速度が0となる剛壁上で振動の最大値（腹）が生じ、粒子速度の振幅が最大（腹）となる点で逆に振動の最小値（節）を生じていることに十分注意すること。これは吸音材の最適な配置計画、施工等の際に考慮すべき事項である。

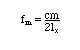
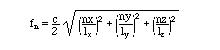
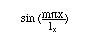
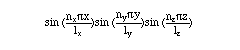
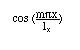
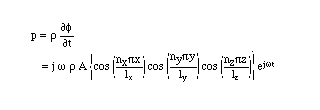
さて、この３次元音場の固有振動はｎx, ｎy, ｎz　の任意の組合わせによって次のように３種類に分類される。

5.1.1　一次元モード　 (axial mode, axial wave)


ｎx, ｎy, ｎzのうち2個が０となるもので、軸波とよばれる。


5.1.2　二次元モード　 (tangential mode, tangential wave)


３個のｎのうち、一個が０となり、接線波とよばれる。


5.1.3　三次元モード　(oblique mode, oblique wave)


三個のｎがいずれも０でないもので、斜め波とよばれる。