定在波 [standing wave]
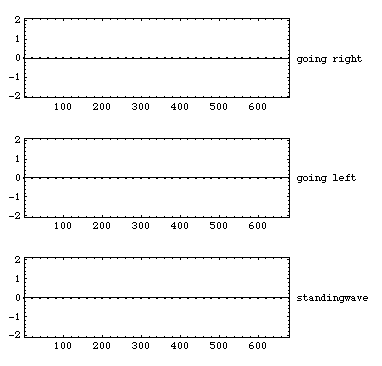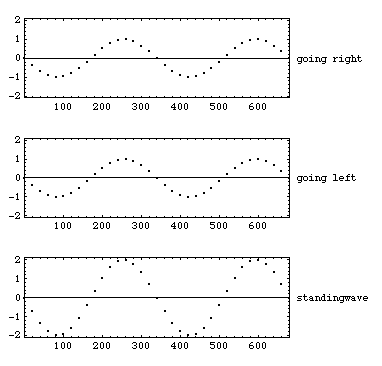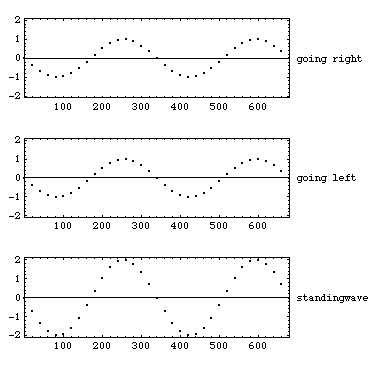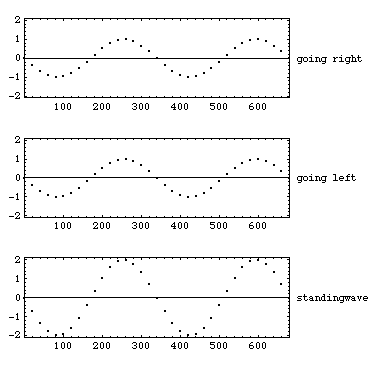
アニメーションの横軸は x(位置)、縦軸は v(粒子速度)を示す。1番目の図では左側から、中央の図では右側から、振幅が等しい同一周波数の純音(正弦波)が出力され、それぞれ右側(x軸の+方向)及び左側(x軸の-方向)へと進む。これら2つの波を単純に足し合わせたものが3番目の図である。二つの波が混ざり合い干渉し合い定常状態へ達した結果、見かけ上進行しない波(定在波)を生じる。また定常状態では、両端でv=0となっている。
この場合、音圧は粒子速度とは逆に、vが0の点で最大値、vが最大値の点で0となる。また音源は最初から最後まで同一の正弦波を同一の大きさで出力し続けている。
考えてみよう。進行方向が異なる振幅が等しい同一周波数の純音が出会うと、お互いに干渉して定在波が生じる。それでは剛壁が左右いずれか片方だけにある場合はどうだろう。
(ヒント)剛壁の定義等は 4.1章を参照。 また詳しい例題が4.2.2 にある。ここでは、粒子速度に関し 剛壁の位置で 、
[反射波の振幅] = -1 × [入射波の振幅]
であり、(当然だが)波の進行方向が逆転する点に注意し、またその結果、
[合成波の振幅] = [入射波 の振幅] + [反射波 の振幅] = 0
となることを理解すること。理解の一助となるように、4.2.2の例題では「剛壁」と対比的な「軟壁」についても言及している。
さて、上記の問いへの答えは以下である。即ち、剛壁へ純音が入射すれば、進行方向が反対で振幅(の絶対値)が等しい音が逆方向へ返ってくるため、両者が干渉し定在波を生じる。かつ、剛壁の位置で粒子速度の振幅が常に「0(ゼロ)」となる。
それでは左右両方に剛壁がある場合はどうなるであろうか。これは各自で考えてみること。