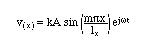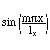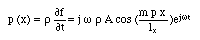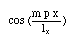CHAP4.html
4
一次元音場の固有モード
- 4.1 閉管内の音場
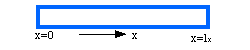
- ここでは、管が x=0と lx において剛壁で閉じられている場合を考える。この空間の「両端が剛壁」という境界条件は、x=0およびx=lxにおいて粒子速度が0でなければならない、ということを意味する。ここで、一次元音 場の波動方程式は2で示したとおり、
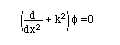 であった。これを満たす解φは前進波と後退波から構成される
であった。これを満たす解φは前進波と後退波から構成される
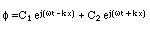 で表されることも既に述べた。あるいは、
で表されることも既に述べた。あるいは、
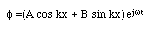 と変形した式でもよい。
と変形した式でもよい。
さて、粒子速度vは、-φをxで微分すれば得られる。即ち、
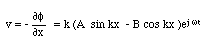 剛壁の条件より閉管の一方の端x=0 では t によらず常にv=0となる。従ってまず、
剛壁の条件より閉管の一方の端x=0 では t によらず常にv=0となる。従ってまず、
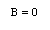 が得られる。あわせて他方の端x=lx で常にv=0となるから、
が得られる。あわせて他方の端x=lx で常にv=0となるから、
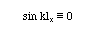 が成立しなければならない。従って、この音場が安定して存在するためには
が成立しなければならない。従って、この音場が安定して存在するためには
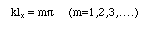 が恒等的に成立する必要があり、これを満たす波長定数は次のような「とびとびの」値となる。
が恒等的に成立する必要があり、これを満たす波長定数は次のような「とびとびの」値となる。
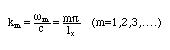 即ち、角周波数ωm、周波数fmは、それぞれ
即ち、角周波数ωm、周波数fmは、それぞれ
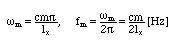
 を満足することになる。この周波数 fmを固有周波数(normal frequency またはnatural frequency)と呼び、この固有振動のことを振動の基準形あるいは固有モード(normal mode of vibration)という。なお、この周波数で管が共鳴することから、この周波数を共鳴周波数とも呼ぶ。
を満足することになる。この周波数 fmを固有周波数(normal frequency またはnatural frequency)と呼び、この固有振動のことを振動の基準形あるいは固有モード(normal mode of vibration)という。なお、この周波数で管が共鳴することから、この周波数を共鳴周波数とも呼ぶ。
ゆえに、この管内の音場、具体的には粒子速度分布と音圧分布は、それぞれ以下のようになる。
まず粒子速度分布は、
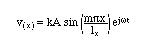 となり、時間項を無視した振幅の分布(の形状)が
となり、時間項を無視した振幅の分布(の形状)が
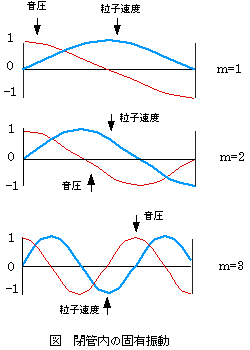
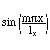 で表され、m=1〜3の時、図のようになる。
で表され、m=1〜3の時、図のようになる。
一方、音圧分布は、
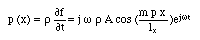 で、同じく振幅の分布(形状)は
で、同じく振幅の分布(形状)は
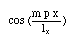 で表され、m=1〜3の時、図のようになる。
で表され、m=1〜3の時、図のようになる。
これらに時間項の影響を加味してアニメーションとして示しているが、このように整数mに対応する特定の固有周波数でこの管内の音圧や粒子速度の分布は、時間とともに進行することのない波、即ち「定在波」(standing wave)となる。この固有モード(あるいは、定在波)は、壁に囲まれた室内の音場を検討する際にも留意すべき重要な現象である。
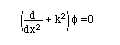
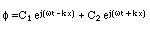
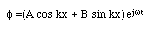
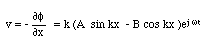
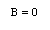
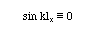
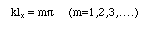
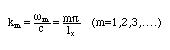
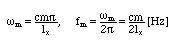
 を満足することになる。この周波数 fmを固有周波数(normal frequency またはnatural frequency)と呼び、この固有振動のことを振動の基準形あるいは固有モード(normal mode of vibration)という。なお、この周波数で管が共鳴することから、この周波数を共鳴周波数とも呼ぶ。
を満足することになる。この周波数 fmを固有周波数(normal frequency またはnatural frequency)と呼び、この固有振動のことを振動の基準形あるいは固有モード(normal mode of vibration)という。なお、この周波数で管が共鳴することから、この周波数を共鳴周波数とも呼ぶ。