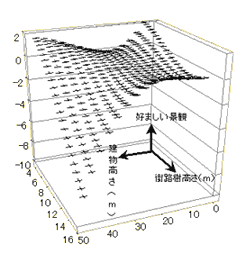
街路景観の総合評価項目「好ましい-好ましくない」と物理量である建物高さと街路樹高さの関係性を明らかにするため、総合評価項目を目的変数Ｚとし、建物高さをＢ、街路樹高さをＴとして、曲面回帰分析を行った。 　

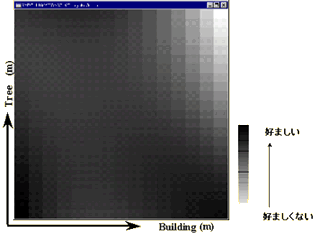
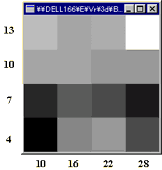
その結果を濃淡図として図９に示す。この濃淡図は、建物高さをＸ軸に街路樹高さをＹ軸にとり、総合評価「好ましい」の高低を濃淡で表すものである。濃淡が濃くなるにつれて総合評価は高くなる。この濃淡図は、評価実験によって得られた実測値と、２次と３次の曲面回帰分析によって得られた予測値を用いて、それぞれ作成したものである。この濃淡図を見ると、３次曲面の濃淡が実測値に非常に類似した傾向を示していることが分かる。従って、３次の曲面回帰分析による予測値が街路景観評価の予測として有効であると思われる。 　

街
路
樹
高
さ
（ｍ）
↑

以上のことから３次の曲面回帰分析について詳しく述べることにする。その結果を表７に示す。
この分析によって得られた回帰式は Ｚ＝-1.926+0.00580Ｔ３-0.147Ｔ２-0.00121Ｔ２Ｂ +0.000268ＴＢ２+0.0175ＴＢ＋1.068Ｔ-0.115Ｂ+0.0000368Ｂ３ となる。 　

さらに、求めた回帰式を３次元グラフに表し（図10）、さらに濃淡図を作成した（図11）。この３次元グラフから、建物と街路樹の高さが高くなるにつれて、街路の総合評価が低くなり、被験者は「好ましくない」と感じることが予測される。また、濃淡図から、濃淡図の斜め中央にかけて、濃淡が濃くなっていることからそこが被験者の総合評価のピークになることが予測される。

非標準化係数

標準化係数

有意水準

相関係数

定数

-1.926

0.000

0.119

0.000

Ｂの定数

-0.115

-0.543

0.160

0.063

Ｂ3

0.000

0.105

0.749

0.079

Ｔ

1.068

2.569

0.027

-0.146

Ｔ2

-0.147

-6.083

0.014

-0.155

Ｔ2Ｂ

-0.001

-0.743

0.086

-0.032

Ｔ3

0.006

3.418

0.012

-0.157

ＴＢ

0.017

0.848

0.284

0.005

ＴＢ2

0.000

0.317

0.522

0.051

重相関係数

0.218

求めた３次曲面の回帰式から、建物高さ22ｍ(７階)の場合を例にとり街路樹高さと街路景観評価の予測を行う。
その場合の回帰式は Ｚ＝0.00580Ｔ３-0.174Ｔ２＋1.583Ｔ-4.064 となり、さらに微分を行うと dＺ/dT＝0.0174Ｔ2-0.347Ｔ+1.583　となる。 　
dＺ/dT＝0の時、Ｔ＝7.048、12.906となることから建物高さ22ｍの場合、街路樹高さが7ｍの時に街路景観評価が高くなり、人が「好ましい」と感じることが分かる。逆に、13ｍの時に低くなり、人が「好ましくない」と感じることが分かる。